二叉树的层序遍历(广度优先遍历)
link:102. 二叉树的层序遍历 - 力扣(LeetCode)
思路分析
题目说明从左往右进行遍历,其实可以堪称给二叉树每一层都画横线分割开来,left first,right last.
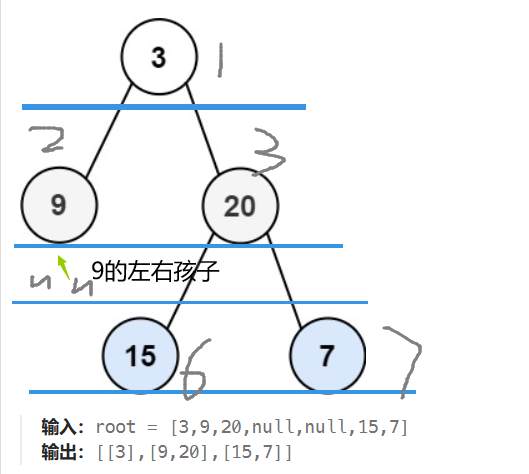
n代表null 输出只从存在的节点中输出.
最先想到的就是递归,按照创建树的思路,pass掉空节点就好.
先前做过队列模拟栈,其实这里用队列来解决也很优雅.
队列BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ret = new ArrayList<>();
if(root == null) {
return ret;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
int size = queue.size();
List<Integer> tmp = new ArrayList<>();
while(size != 0) {
TreeNode cur = queue.poll();
tmp.add(cur.val);
size--;
if(cur.left != null) {
queue.offer(cur.left);
}
if(cur.right != null) {
queue.offer(cur.right);
}
}
ret.add(tmp);
}
return ret;
}
}
|
Tips
高度:二叉树中任意一个节点到叶子结点的距离
深度:二叉树中任意一个节点到根节点的距离
List<List<Integer>> 的必要性
每一层的节点值需要单独存储在一个列表中,然后将所有层的列表整合在一个大列表中。因此,最终结果需要一个嵌套的列表结构。
反转二叉树
link:226. 翻转二叉树 - 力扣(LeetCode)
思路分析
根据题意,看到的是左右子树内部交换自身孩子节点,然后左右子树又进行了交换.
递归交换就秒了.
其实可以老老实实的逐个左右交换,也可以按照上一题层序遍历的一层层交换(观察到最后一层是1,3,6,9——>9,6,3,1)
DFS(递归)
注意前序遍历和后序遍历可以,中序遍历不行(不信你就画图推推看)
前序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution {
public TreeNode invertTree(TreeNode root) {
if(root == null) {
return null;
}
TreeNode tmp = root.left;
root.left= root.right ;
root.right = tmp;
invertTree(root.left);
invertTree(root.right);
return root;
}
}
|
后序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
TreeNode left = invertTree(root.left);
TreeNode right = invertTree(root.right);
root.left = right;
root.right = left;
return root;
}
}
|
BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {return null;}
ArrayDeque<TreeNode> deque = new ArrayDeque<>();
deque.offer(root);
while (!deque.isEmpty()) {
int size = deque.size();
while (size-- > 0) {
TreeNode node = deque.poll();
swap(node);
if (node.left != null) {deque.offer(node.left);}
if (node.right != null) {deque.offer(node.right);}
}
}
return root;
}
public void swap(TreeNode root) {
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
}
}
|
Tips
人机有话说.
DFS 和 BFS 的区别
- 遍历顺序
- DFS(Depth First Search,深度优先搜索):优先深入到每个节点的子节点,通常会先访问到某个分支的最底层节点,然后再回溯到上层节点去访问其他分支。常见的 DFS 实现有三种:前序遍历(Preorder)、中序遍历(Inorder)、后序遍历(Postorder)。
- BFS(Breadth First Search,广度优先搜索):优先访问每一层的节点,然后再逐层深入。BFS 一般使用队列(
Queue)来实现,按层次逐一处理节点。
- 数据结构
- DFS:常用递归或栈来实现,递归会隐式使用系统栈,而非递归的实现需要显式的栈。
- BFS:通常使用队列来实现,因为它按照层次顺序访问节点。
- 时间复杂度和空间复杂度
- 时间复杂度:DFS 和 BFS 的时间复杂度都是 O(n),其中 nnn 是节点的数量,因为每个节点都需要被访问一次。
- 空间复杂度:DFS 的空间复杂度取决于递归的深度,最坏情况下是 O(h)(树的高度);BFS 的空间复杂度则是 O(w),其中 w是树的最大宽度。
对称二叉树
link:101. 对称二叉树 - 力扣(LeetCode)
思路分析
看题目确实觉得很对称啊,看图分析左子树和右子树的遍历顺序,左子树是左右中,那和右子树比较的时候就是右左中.
特殊情况优先考虑
左空右空->true
左不空右空->false
左空右不空->false
那最后的情况就是左右都不为空了,这时候就需要单独判断.
单侧不对称就可以返回false.
那么这么比较就只能是后序遍历了.
递归秒!
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Solution {
public boolean isSymmetric(TreeNode root) {
return cmp(root.left,root.right);
}
boolean cmp(TreeNode left,TreeNode right) {
if(left == null && right == null) {
return true;
}else if(left == null && right != null) {
return false;
}else if(left != null && right == null) {
return false;
}else if(right.val != left.val){
return false;
}
boolean last = cmp(left.left,right.right);
boolean lastnext = cmp(left.right,right.left);
return last && lastnext;
}
}
|
注意
不要else if判断结束之后直接else{return true;}
这样做的话没有判断其他剩余的子节点 ,意味着中层节点的值心相等,但是叶子节点的值不通,但仍然判断这种情况为true,这样是不对的.


