找树左下角的值
link:513. 找树左下角的值 - 力扣(LeetCode)
思路分析
看题目给出的样例分析,觉得可以从深度入手.如果是左子树深度最大,那直接输出最左边的左子树节点即可(只有一个左节点的话也是如出一辙)
又假设二叉树中至少有一个节点,就已经列举出一种特殊需要判断的情况了.
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
class Solution {
int result = 0;
int Deepth = -1;
public int findBottomLeftValue(TreeNode root) {
result = root.val;
exrloration(root,0);
return result;
}
public void exrloration(TreeNode node,int deepth) {
if(node == null) {
return ;
}
if(node.left == null && node.right == null) {
if(deepth > Deepth) {
Deepth = deepth;
result = node.val;
}
}
if(node.left != null) {
exrloration(node.left,deepth+1);
}
if(node.right!= null) {
exrloration(node.right,deepth+1);
}
}
}
|
路径总和
link:112. 路径总和 - 力扣(LeetCode)
思路分析
类似数组遍历求和(滑动窗口)找目标总和值只不过换成二叉树.
首先还是想到按照前序遍历的方式,递归遍历.由于根节点是一定要选中的,(null另算)那我们遍历子节点做差判断最后是否等于0即可.
或者可以从下向上按照层,借助队列实现二叉树版滑动窗口.🤔
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root == null) {
return false;
}
targetSum -= root.val;
if(root.left == null && root.right == null) {
return targetSum == 0;
}
if(root.left != null){
boolean left = hasPathSum(root.left,targetSum);
if(left) {
return true;
}
}
if(root.right != null){
boolean right = hasPathSum(root.right,targetSum);
if(right) {
return true;
}
}
return false;
}
}
|
从中序和后序遍历构造二叉树
link:106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
思路分析
其实和我们数据结构考试中的内容一致,画图推推规律.
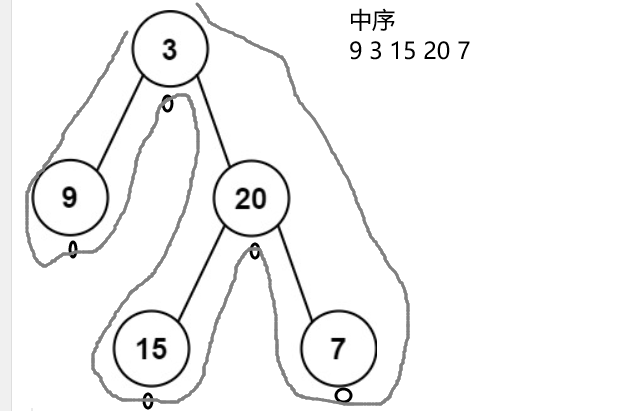
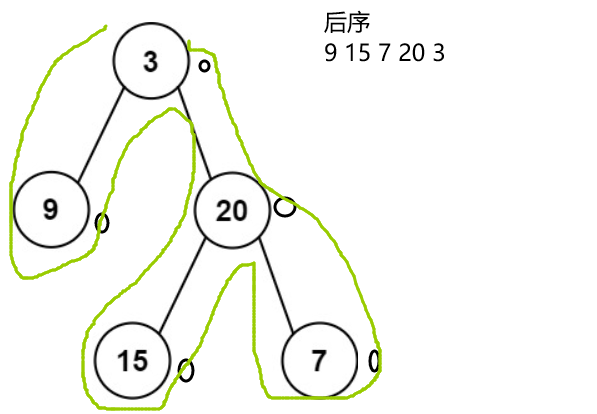
根据画图规律可得 后续遍历中root位置出现在最后一个位置,再结合中序遍历可以得出9为左子树,15、20、7为右子树.
我使用Map进行解决,key存储值,value存储下标.
中序遍历中root的index + 1.
根据之前分析的规律,我们利用后序遍历确定root.value,然后对应在中序遍历中定位到root位置(利用index)然后回溯到中序遍历切割出左子树那么在后序遍历中剩余的部分就是右子树.
Map
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
Map<Integer,Integer> map;
public TreeNode buildTree(int[] inorder, int[] postorder) {
map = new HashMap<>();
for(int i = 0;i<inorder.length;i++)
{
map.put(inorder[i],i);
}
return FindOrder(inorder,0,inorder.length,postorder,0,postorder.length);
}
public TreeNode FindOrder(int[] inOrder,int inBegin,int inEnd,int[] postOrder,int postBegin,int postEnd)
{
if(inBegin>=inEnd || postBegin>=postEnd)
{
return null;
}
int index = map.get(postOrder[postEnd - 1]);
TreeNode root = new TreeNode(inOrder[index]);
int lenOfLeft = index - inBegin;
root.left = FindOrder(inOrder,inBegin,index,postOrder,postBegin,postBegin+lenOfLeft);
root.right = FindOrder(inOrder,index+1,inEnd,postOrder,postBegin+lenOfLeft,postEnd-1);
return root;
}
}
|
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| class Solution {
public int postIndex;
public TreeNode buildTree(int[] inorder, int[] postorder) {
postIndex = postorder.length-1;
return buildTreeChild(postorder,inorder,0,inorder.length-1);
}
private TreeNode buildTreeChild(int[] postorder,int[] inorder,int inbegin,int inend) {
if(inbegin > inend) {
return null;
}
TreeNode root = new TreeNode(postorder[postIndex]);
int rootIndex = findIndex(inorder,inbegin,inend,postorder[postIndex]);
if(rootIndex == -1) {
return null;
}
postIndex--;
root.right = buildTreeChild(postorder,inorder,rootIndex+1,inend);
root.left = buildTreeChild(postorder,inorder,inbegin,rootIndex-1);
return root;
}
private int findIndex(int[] inorder,int inbegin,int inend,int key) {
for(int i = inbegin;i <= inend;i++) {
if(inorder[i] == key) {
return i;
}
}
return -1;
}
}
|
Tips
理解构建过程的示例
以中序遍历 inorder = [9, 3, 15, 20, 7] 和后序遍历 postorder = [9, 15, 7, 20, 3] 为例:
- 第一次调用:
postIndex 指向 3,创建根节点 3.- 在中序数组中找到
3 的索引为 1.
- 右子树范围
[15, 20, 7],左子树范围 [9].
- 构建右子树:
- 递归调用构建右子树,
postIndex 现在指向 20,创建节点 20.
- 在中序数组中找到
20 的索引为 3.
- 构建左子树(对于
20):
- 继续递归构建右子树(此时后序的下一节点是
7).
- 处理完
20 的右子树后,回溯到 20,然后处理 20 的左子树(为 15).
- 构建左子树(对于
3):
- 现在回到根节点
3,处理左子树(此时后序的下一节点是 9).



