yubのAlgorithm.0x16

修建二叉搜索树

link：669. 修剪二叉搜索树 - 力扣（LeetCode）

思路分析

注意修剪的时候要考虑到全部的节点，即搜到到限定区间小于左值或者大于右值时还需要检查当前不符合区间大小节点的右子树/左子树，不能直接返回null.
剪去节点只需要在判断当前节点左/右子树后将root的左/右节点更新即可.

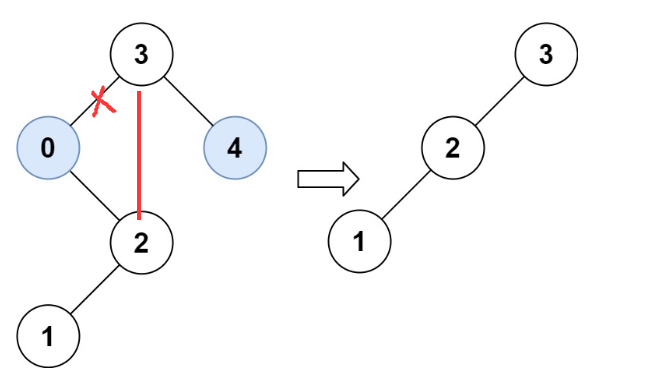
递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if(root == null) {
            return null;
        }
        if(root.val < low) {
            return trimBST(root.right,low,high);
        }
        if(root.val > high) {
            return trimBST(root.left,low,high);
        }
        root.left = trimBST(root.left,low,high);
        root.right = trimBST(root.right,low,high);
        return root;
    }
}

将有序数组转化为平衡二叉树

link：108. 将有序数组转换为二叉搜索树 - 力扣（LeetCode）

思路分析

给了升序数组其实一开始想的也是第一个参数是左子树最左边的值，然后去选中间节点做切割.
具体就需要怎么在偶数和奇数参数个数下都适配，其实偶数情况无非是选取中间的两个数（left + (right - left) / 2）.

题目给的输入输出示例其实也已经帮我们提供了两种思路.

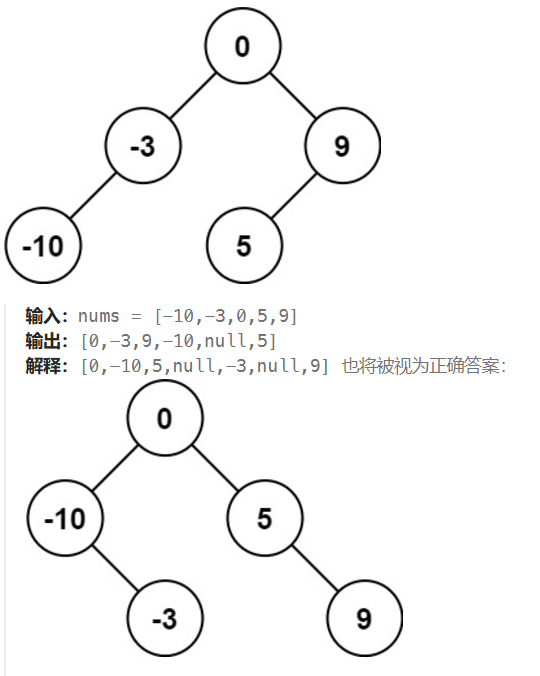
递归+双指针

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
//采用左闭右闭区间
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
         return sort(nums,0,nums.length - 1);  
    }
    TreeNode sort(int[] nums, int left, int right) {
        if(left > right) {
            return null;
        }
        int mid = left + ((right - left) >> 1);
        TreeNode root = new TreeNode(nums[mid]);
        root.left = sort(nums,left,mid - 1);
        root.right = sort(nums,mid + 1,right);
        return root;
    }
}

把二叉搜索树转换为累加树

link：538. 把二叉搜索树转换为累加树 - 力扣（LeetCode）

思路分析

第一遍看题目还有点没看明白（挠头.jpg
其实就是对于树中的每个节点，计算它的值加上树中所有大于该节点值的节点的值.但是保证搜索二叉树的定义，那就是左子树的节点值必须小于节点的值，右子树的节点值必须大于节点的值.那我们就从右子树入手，反向中序遍历（右根左)，确保累加时考虑了所有大于当前节点的值.
和上一题相同的思路.

递归+双指针

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int pre = 0;
    public TreeNode convertBST(TreeNode root) {
        travsal(root);
        return root;
    }
   void travsal(TreeNode root) {
    if (root == null) {
        return; // 如果当前节点为空，直接返回
    }
    travsal(root.right);  // 先遍历右子树
    root.val += pre;      // 将当前节点的值加上pre
    pre = root.val;       // 更新pre为当前节点的新值
    travsal(root.left);   // 再遍历左子树
   }
}