初探回溯

什么是回溯算法

回溯算法是一种暴力穷举的搜索方式.
回溯和递归是相辅相承的**.(有递归就会有回溯)**

回溯法解决的问题
  • 组合问题：N个数里面按一定规则找出k个数的集合.
  • 切割问题：一个字符串按一定规则有几种切割方式.
  • 子集问题：一个N个数的集合里有多少符合条件的子集.
  • 排列问题：N个数按一定规则全排列，有几种排列方式.
  • 棋盘问题：N皇后，解数独等.
使用回溯算法解决问题的思路

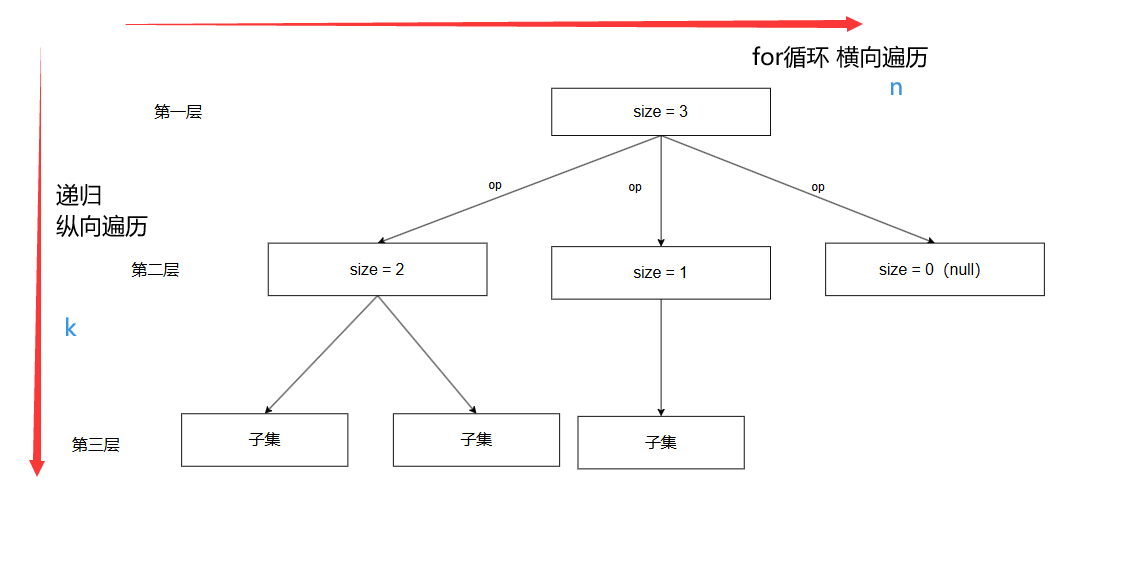
虽然回溯算法暴力效率低下理解起来更为抽象，但好在天无绝人之路，回溯算法的问题都可以用树形结构来进行理解.

关键有以下两点：
1.集合大小->树的宽度
2.递归深度->树的深度
image-20241121153238086

1
2
3
4
5
6
7
8
9
10
11
12
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

组合问题

link：77. 组合 - 力扣（LeetCode）

思路分析

进入到回溯算法的学习！

首先明确是在求组合，组合中的元素是不能重复的.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    List<Integer> path = new ArrayList<>();
    List<List<Integer>>  result = new ArrayList<>();
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n,k,1);
        return result;
 
    }
    public void backtracking(int n, int k,int startIndex)
    {
        //终止条件
        if(path.size() == k)
        {
            result.add(new ArrayList<>(path));
            return;
        }
        //for循环
        for(int i = startIndex;i<=n;i++)
        {
            path.add(i);
            backtracking(n,k,i+1);
            path.remove(path.size()-1);
        }
    }
}

优化思路
当我们n=k时，第一层for循环再往后遍历就没有意义了.（因为我们最终要取的数的数量要满足，从第二层开始往后的for循环其实已经自动减少了集合中的子集数量，显然这是不符合预期的）
以下引用代码随想录分析图
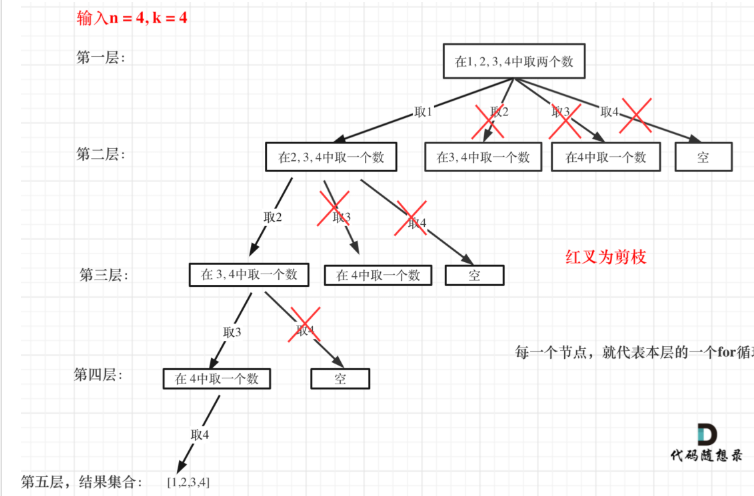
image-20241121150939192

优化部分

1
2
3
1.已经选择的元素个数：path.size();
2.还需要的元素个数为: k - path.size();
3.在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

优化之后的for循环代码

1
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    List<Integer> path = new ArrayList<>();
    List<List<Integer>>  result = new ArrayList<>();
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n,k,1);
        return result;
    }
    public void backtracking(int n, int k,int startIndex)
    {
        //终止条件
        if(path.size() == k)
        {
         //new ArrayList(path)，创建了 path 的一个副本
   //这意味着即使后续对 path 的修改也不会影响到 result 中已经保存的组合
            result.add(new ArrayList<>(path));
            return;
        }
        //for循环
        for(int i = startIndex;i <= n - (k - path.size()) + 1;i++)
        {
            path.add(i);
            backtracking(n,k,i+1);
            path.removeLast();
        }
    }
}