组合总和
link:39. 组合总和 - 力扣(LeetCode)
思路分析
其实思路和昨天的很像,但是元素可以复用而且也不是字符串.
那还是依旧使用path进行记录,res进行返回结果,sum进行统计最后再加上一个标记位置进行判断即可.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
List<Integer> path = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
int startIndex = 0;
backstracking(candidates, target, sum, startIndex);
return res;
}
int sum = 0;
public void backstracking(int[] candidates, int target, int sum, int startIndex) {
if(sum > target) {
return;
}
if(sum == target) {
res.add(new ArrayList(path));
return;
}
for(int i = startIndex; i < candidates.length; i++) {
path.add(candidates[i]);
sum += candidates[i];
backstracking(candidates,target,sum,i);
sum -= candidates[i];
path.remove(path.size() - 1);
}
}
}
|
组合总和II
link:40. 组合总和 II - 力扣(LeetCode)
思路分析
上一题的plus版,最开始想的是和上一题的思路相同加一个set去掉重复的集合结果会超时…(菜就多练)
这里就出现了一个新知识点——学会加标识辅助数组.(苦笑)
潦草的分析图
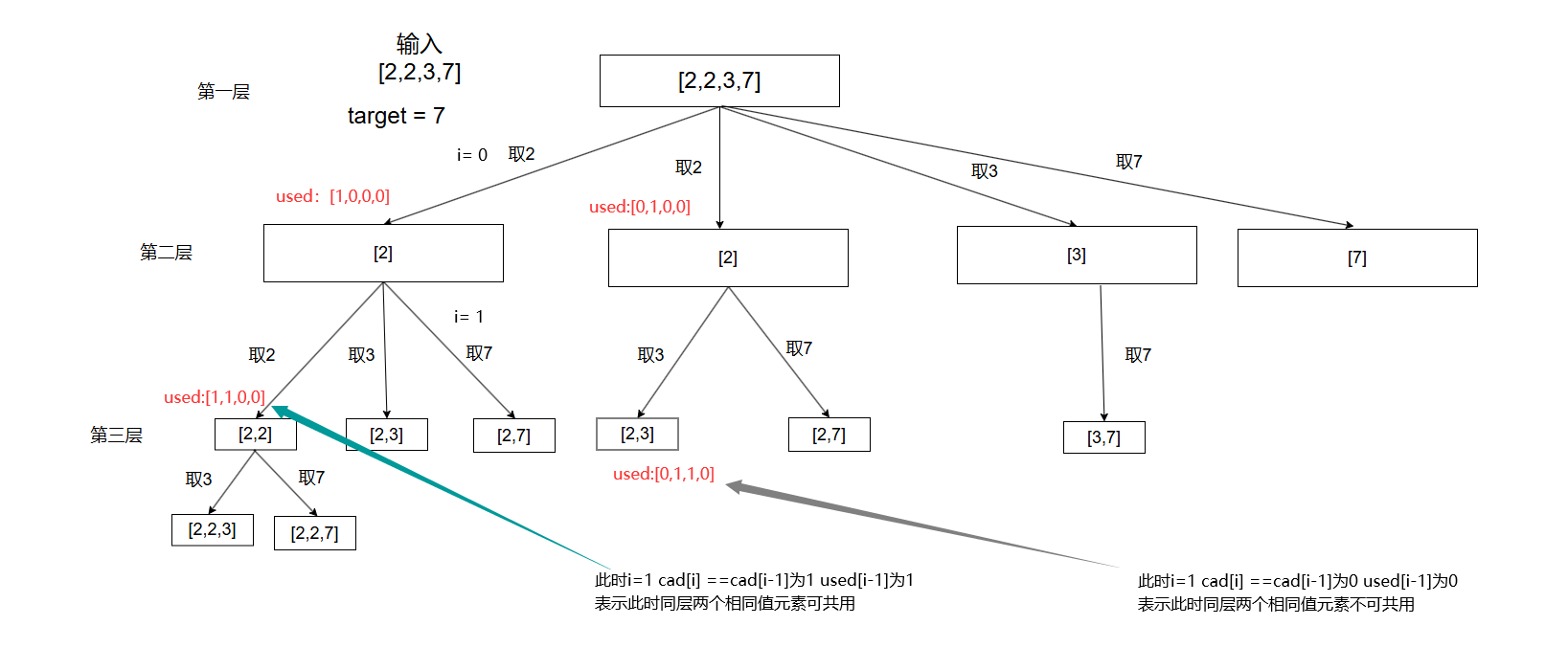 我们需要额外创建一个boolean的used数组来记录当前的位置是否被用过
我们需要额外创建一个boolean的used数组来记录当前的位置是否被用过
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
List<Integer> path = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
int sum = 0;
boolean[] used;
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
used = new boolean[candidates.length];
Arrays.fill(used,false);
Arrays.sort(candidates);
backstracking(candidates,target,0);
return res;
}
public void backstracking(int[] candidates, int target,int startIndex) {
if(sum == target) {
res.add(new ArrayList(path));
return;
}
for(int i = startIndex; i < candidates.length; i++) {
if(sum + candidates[i] > target) {
break;
}
if(i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {
continue;
}
used[i] = true;
sum += candidates[i];
path.add(candidates[i]);
backstracking(candidates, target, i + 1);
used[i] = false;
sum -= candidates[i];
path.remove(path.size() - 1);
}
}
}
|
Tips
去掉 candidates[i] == candidates[i - 1],会导致无法判断相邻重复元素,生成重复的组合.
完整逻辑:
candidates[i] == candidates[i - 1]:用于识别相邻的重复元素。!used[i - 1]:确保同一层中,跳过未使用的重复元素。
 我们需要额外创建一个boolean的used数组来记录当前的位置是否被用过
我们需要额外创建一个boolean的used数组来记录当前的位置是否被用过